Best Casino Roulette Numbers
I recently read a post by another gambling writer who offers a roulette strategy. He makes the following claim about this “big number roulette strategy:”
- Best Casino Roulette Numbers Games
- Best Casino Roulette Numbers Generator
- Best Casino Roulette Numbers Game
The Roulette Number program is a great way to learn Roulette game for online casinos. Best of all is that the software can play instead of you at about 250 casinos. Roulette Number is used worldwide, UK, USA, Germany, Russia, Italy, Czech Republic, France, Portugal, Poland and so on. Dear Sir, In a single zero roulette game, the PROBABILTY of winning increases if you place a portion of your money on fewer numbers for more spins versus covering more numbers per spin, an example: If you are willing to risk 500$ in order to win 250$ then you could: Option (A): place 250$ on any of two dozen and should you be a winner you will.
If you use these 2 roulette tricks and combine them with my money management advice, you might reduce the overall negative expectation of the game.
He starts the post by rambling about dice games during the time of Caesar, which seems to be a digression. He follows up by explaining the difference between a roulette trick and a roulette system.
The conclusion he comes to is that there isn’t much of a difference between roulette tricks and roulette systems. A trick, basically, is less complicated than a system.
The idea behind the big number roulette strategy is that you look at the numbers which have hit over the last 20 spins. These are usually posted digitally above the roulette table. You look for a number which has hit multiple times.
The number that’s hit the most often is “the big number.”
When you sit down at the roulette table, you start betting on that big number.
You sit down at the roulette table, and out of the last 20 spins, the number 20 has come up 3 times. The 8 has come up twice, too.
Since both these numbers are “repeaters,” you’re going to bet on each of them each spin.
The Size of Your Bets Using this Roulette Trick
This would be a boring roulette trick if it were this simple, so the blogger includes some additional advice about how to size your bets.
If you’re betting the table minimum, you just place the minimum sized bet on each number.
If you usually bet more than the table minimum, you divide the size of your usual bet by the number of bets you’re making. You’ll rarely be betting on more than 3 numbers at one time, so your bet sizes will usually work like this:
If you’re betting on one number, you’ll just place your normal sized bet.
If you’re betting on 2 numbers, you’ll just bet half of your normal sized bet on each number.
If you’re betting on 3 numbers, you’ll bet about 1/3 of your normal sized bet on each number.
When to Stop Betting with this Trick
The next part of the trick to keep in mind is that you’re supposed to watch the “scoreboard.” When a number disappears from the scoreboard, you stop betting on it.
It’s possible that at some point there won’t be any repeaters on the scoreboard. When that happens, you stop betting until one of the numbers has started repeating.
His premise is that it takes self-discipline to stop betting. This is true, although—as I’ll explain shortly—it’s not impressive to exercise self-discipline when you’re using a faulty strategy.
The only advantage to sitting out a few rounds of betting is that you’re putting less money into action. Anything you can do to reduce the number of bets you place per hour lowers your predicted hourly loss rate.
Negative Betting
He goes on to explain that some players prefer to bet against numbers which have come up multiple times already. He calls this “negative betting.”
The language he uses to describe this is interesting. He says that this approach is “just as valid” as the strategy he’s presenting.
On this, I agree with him.
Betting on a number because it’s come up repeatedly does nothing to improve your odds. Betting against numbers that have already come up does nothing to improve your odds, either.
I’ll have more to say about that shortly, too, but I want to make sure I do a good job of making the case for the big number strategy before offering my critique of it.
Multiple Numbers Repeating a Different Number of Times
I guess one of the questions some roulette players ask about this system is what they should do if multiple numbers have shown up repeatedly but with a different frequency.
For example, if one number has come up 4 times, another number has come up 3 times, and a 3rd number has come up twice, should you change your betting strategy?
The writer’s advice is to stick with the same flat betting amount on each number. The idea is to keep it simple.
Then he offers the most honest piece of information in the entire description of the strategy:
Best Casino Roulette Numbers Games
It’s almost as if this writer has multiple personalities, because the implication is that you are doing something worthwhile by betting on the number that’s come up repeatedly.
But according to his statement about the probabilities, you could just bet on any number you want every time you spin the wheel. And there would be no difference.
Other Bets Besides the Straight Up Bet
He goes on to explain that you’re not locked into making the straight single-number bet. That has the best payout (35 to 1), but you can place other bets based on the big number that will hit more frequently, albeit with lower payouts.
Let’s say, for example, that the black 10 has come up repeatedly.
You could place the following bets, all of which pay out at even money—and all of which win closer to 50% of the time:
- You can bet on black.
- You can bet on even.
- You can bet on low.
If you place all 3 of those bets and that black 10 hits again, you’ll win all 3 bets.
You could even place those bets along with some more aggressive bets, like a bet on 1-12, which pays off at 2 to 1. You could even bet the single-number bet in addition to these other bets.
Of course, if you have multiple repeaters, you might be prevented from making some of these bets. If there’s a red repeater AND a black repeater, you wouldn’t bet on black (or red).
Some Tips to Keep in Mind When Using the Big Number Roulette System
He also offers some more tips from his perspective as a “conservative player:”
- Don’t make too many bets at the same time. (He doesn’t explain how many bets are too many, though.)
- Don’t increase the size of your bets when you’re losing. (This is good advice, actually, although it doesn’t matter as much as you might think. After all, when you’re playing a negative expectation game like roulette, you’ll lose all your money eventually anyway if you keep playing.)
- Don’t bet so much money that you’ll be upset if you lose it. (This is also good advice, actually. You shouldn’t be gambling with money you can’t afford to lose, ever.)
- Keep your gambling money in a separate bank account. (This is meant to prevent you from mixing your living expenses with your gambling bankroll. I think this is overkill. It reminds me of some of the strategies alcoholics use to try to reign in their drinking. Those strategies never work, by the way. I promise.)
What’s Wrong with this Roulette Strategy?
This post about the big number roulette strategy was one of the stranger posts about roulette strategy that I’ve ever read, because it never gives any justification for why you would want to use this strategy.
I can surmise—based on reading one of the blogger’s books in print—that the idea is to take advantage of a biased wheel, but he doesn’t explain that in the post. He just says, hey, here’s a neat way to bet on roulette that might decrease your negative expectation.
His strategy doesn’t do that, by the way, but I’ll finish his argument for him below:
And by betting on that number, you’re taking advantage of that imperfection.
How Realistic Is It That You’re Going to Find a Biased Wheel in Today’s Casinos?
At one time, casinos did have biased roulette wheels on their floors. You can read numerous accounts of gamblers not only getting an edge but winning lots of money taking advantage of such biased wheels. Some gamblers won millions.
Here’s the thing, though:
Modern casinos run a tight ship. Casino equipment is replaced regularly and moved often. Even if you found a biased wheel, it might not be in the same location during the next shift at the casino.
I’d put the odds of actually finding a biased casino at slim to none to begin with.
How would you know if a wheel were biased?
It would take more than 20 spins to have any kind of confidence that a wheel is anything other than random. In fact, it would take more than 200 spins, too.
You couldn’t reliably expect to have an idea about an imperfection on a roulette wheel unless you observed at least 2000 spins.
Even then, your confidence level should be low. You’d need 5000 to 10,000 spins to realistically predict which numbers come up more often than they should.
Let’s assume that you can observe an average of 50 spins per hour on a roulette wheel. This means a minimum of 40 hours of observation clocking the wheel before you can have any confidence in your results.
You’d be better off, though, with between 100 and 200 hours of observation.
And since the casino moves the wheels around from time to time, you’d need at least one—possibly 2 or 3 confederates to help you clock the results.
That’s a full time job for all 3 of you.
But consider this, too:
You might spend all that time clocking a wheel only to find that there’s no bias at all.
Or you might spend that time clocking a wheel to find a bias, but it’s not enough of a bias to get an edge over the casino. After all, on an American roulette wheel, the house edge is 5.26%. Even if there’s enough of a bias to cut that in half, you’re still facing a significant edge.
Hot Numbers, Cold Numbers, and the Gamblers Fallacy
The Gamblers Fallacy is the belief that previous results affect subsequent results in independent trials.
A spin of a roulette wheel is an independent event. The probability for an independent event is simple—you divide the number of ways you can win by the total possible number of outcomes.
On a roulette wheel, there are 38 different numbers. With a single number bet, only one of those numbers can win, so the probability is 1/38.
The payoff is 35 to 1, so it’s obvious how the house gets its edge. You’ll lose slightly more often than you should to break even, and the house gets to keep the money.
But if the ball lands red 5 times in a row, you’d be forgiven for thinking either of the following:
- You should bet on red, because red is hot and more likely to come up on the 6th
- You should be on black, because black is overdue. It’s unlikely to see red come up 6 times in a row.
Betting on a number because it comes up more often in a set of 20 spins doesn’t change the probability.
Betting against that number doesn’t change the probability either.
Thinking that it does is engaging in the Gamblers Fallacy.
The Problem with So-Called Roulette Strategies like This
Even though the post I read explaining the big number roulette strategy includes multiple disclaimers, it also leads you to believe that you’re somehow going to get an edge over the casino. The author even stated early in the post that even if you can’t get an edge, you might lower your negative expectation.
He contradicts himself later in the post, but at least he was accurate in that later section.

You can’t get an edge at roulette. The house edge for the game is almost carved into stone. It’s not something you can change by following trends.
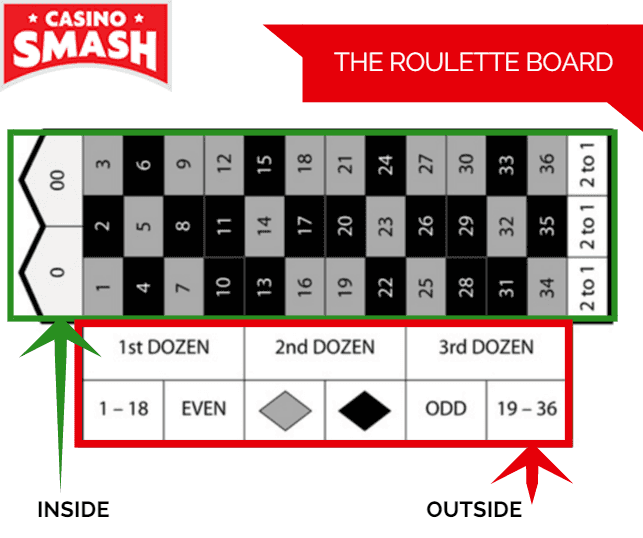
It might be fun to bet this way.
But in no way does it reduce the house’s inherent mathematical edge against you.
Keeping your gambling funds in a separate bank account, watching the size of your bets, and betting on a number that’s come up repeatedly in the last 20 spins does nothing to help you succeed at roulette.
Conclusion
The big number “roulette trick” is just a strategy for betting on roulette that exemplifies the Gamblers Fallacy in action. A big number roulette bettor looks for a number or multiple numbers that have come up repeatedly in the last 20 spins. He then places single number bets on that number. Or he makes broader bets based on the color of the number, or whether it’s even or odd, or whether it’s in the 1st, 2nd or 3rd dozen.
The problem with the strategy is that it doesn’t work in the long run.
Sure, you can sometimes hit a win with a strategy like this.
But your probability of hitting a win with a strategy like this is no better than it would be if you just chose a different number every spin of the wheel.
I don’t like posts that promote this kind of betting strategy, even when such a post includes disclaimers. I want to be really firm about this:
I don’t recommend using the big number roulette strategy.
It doesn’t work in the long run, and it offers no advantages over any other “strategy” for the game. It might be entertaining, but I don’t think it’s much more entertaining than just playing roulette haphazardly.
Introduction
The Gambler's Fallacy is the mistaken belief that if an independent event has not happened in a long time, then it becomes overdue and more likely. It is also equally incorrect that if an outcome has happened a disproportionate number of times lately, compared to statistical expectations, then it becomes overheated and less likely to occur the next time. An example of this fallacious thinking might be that if the number 23 hasn't been drawn in a 6-49 lottery the last 100 games, then it becomes more likely to be drawn during the next drawing.
Many worthless betting strategies and systems are based on belief in the Gambler's Fallacy. I got the idea for writing about this after reading an 888 online roulette article by Frank Scoblete entitled How to Take Advantage of Roulette Hot Spots. In that article, Scoblete recommends taking a count of each outcome for 3,700 spins in single-zero roulette and 3,800 spins in double-zero roulette in the hunt for 'hot numbers.' Never mind that this would take about 100 hours to make this many observations, assuming the industry standard of 38 spins per hour.
Before going further, let me say that I strongly believe modern roulette wheels made by top brands like Cammegh are extremely precise and any bias would be minuscule compared to the house advantage. Thus, testing a modern roulette for bias would be a total waste of time. Now, testing a 30-year-old hand-me-down wheel in a banana republic might be another story. However, you're on your own if you win a lot of money from said casino and try to leave with it.
Best Casino Roulette Numbers Generator
That said, if you track 3,800 outcomes in single-zero roulette, the average number of times any number will hit is 3800/38=100. I ran a simulation of over 1.3 trillion spins, counting how many times each number was hit, sorting the outcomes to find the most frequent number and how many times it was observed, and keeping a count of how many times the most frequent number in each simulation was seen.
Hottest Number in 3,800 Spins of Double-Zero Roulette

As a former actuary, I hate to use a layman's term like the 'hottest number,' but that is how gamblers talk so will go with that. That said, following are the results of the count of the hottest number in millions of 3800-spin simulations.
Count of the Hottest Number in 3,800 Spins on Double-Zero Wheel
| Statistic | Value |
|---|---|
| Mean | 122.02 |
| Median | 121 |
| Mode | 120 |
| 90th Percentile | 128 |
| 95th Percentile | 131 |
| 99th Percentile | 136 |
| 99.9th Percentile | 142 |
Here is what the table above means in plain simple English.
- The mean, or average, count of the hottest number is 122.02.
- The median count of the most frequent number is 121. This means that over 50% of time the most frequent number appeared 121 times or less, as well as 121 times or more. This is possible because the probability of 121 observations is in both groups.
- The mode, or most count of the hottest number is 120, which happens 8.29% of the time.
- The 90th percentile is the smallest number such that the probability the count of the hottest number is at least 90% .
- The 95th percentile is the smallest number such that the probability the count of the hottest number is at least 95%.
- The 99th percentile is the smallest number such that the probability the count of the hottest number is at least 99%.
- The 99.9th percentile is the smallest number such that the probability the count of the hottest number is at least 99.9%.
Hottest Number in 3,700 Spins of Single-Zero Roulette
The results are very similar with 3,700 spins tracked on a single-zero wheel. Following is a summary of the results.
Count of the Hottest Number in 3,700 Spins on Single-Zero Wheel
| Statistic | Value |
|---|---|
| Mean | 121.90 |
| Median | 121 |
| Mode | 120 |
| 90th Percentile | 128 |
| 95th Percentile | 131 |
| 99th Percentile | 136 |
| 99.9th Percentile | 142 |
The following table shows the full results of the simulation on both wheels. The two commulative columns show the probability that the count of the hottest number is the number on the left column or more. For example, the probability the hottest number in 3,700 spins of single-zero roulette is 130 or more is 0.072044.
Summary of the Count of the Hottest Number in 3,700 Spins of Single-Zero Roulette and 3,800 spins of Double-Zero Roulette
| Count | Probability Single Zero | Cummulative Single Zero | Probability Double Zero | Cummulative Double Zero |
|---|---|---|---|---|
| 160 or More | 0.000001 | 0.000001 | 0.000001 | 0.000001 |
| 159 | 0.000000 | 0.000001 | 0.000000 | 0.000001 |
| 158 | 0.000001 | 0.000001 | 0.000001 | 0.000001 |
| 157 | 0.000001 | 0.000002 | 0.000001 | 0.000002 |
| 156 | 0.000001 | 0.000003 | 0.000001 | 0.000003 |
| 155 | 0.000002 | 0.000005 | 0.000002 | 0.000005 |
| 154 | 0.000003 | 0.000009 | 0.000003 | 0.000008 |
| 153 | 0.000005 | 0.000013 | 0.000005 | 0.000013 |
| 152 | 0.000007 | 0.000020 | 0.000008 | 0.000021 |
| 151 | 0.000012 | 0.000032 | 0.000012 | 0.000033 |
| 150 | 0.000017 | 0.000049 | 0.000018 | 0.000051 |
| 149 | 0.000026 | 0.000075 | 0.000027 | 0.000077 |
| 148 | 0.000038 | 0.000114 | 0.000041 | 0.000118 |
| 147 | 0.000060 | 0.000174 | 0.000062 | 0.000180 |
| 146 | 0.000091 | 0.000265 | 0.000092 | 0.000273 |
| 145 | 0.000132 | 0.000397 | 0.000137 | 0.000409 |
| 144 | 0.000195 | 0.000592 | 0.000199 | 0.000608 |
| 143 | 0.000282 | 0.000874 | 0.000289 | 0.000898 |
| 142 | 0.000409 | 0.001283 | 0.000421 | 0.001319 |
| 141 | 0.000580 | 0.001863 | 0.000606 | 0.001925 |
| 140 | 0.000833 | 0.002696 | 0.000860 | 0.002784 |
| 139 | 0.001186 | 0.003882 | 0.001215 | 0.003999 |
| 138 | 0.001652 | 0.005534 | 0.001704 | 0.005703 |
| 137 | 0.002315 | 0.007849 | 0.002374 | 0.008077 |
| 136 | 0.003175 | 0.011023 | 0.003286 | 0.011363 |
| 135 | 0.004355 | 0.015378 | 0.004489 | 0.015852 |
| 134 | 0.005916 | 0.021295 | 0.006088 | 0.021940 |
| 133 | 0.007939 | 0.029233 | 0.008196 | 0.030136 |
| 132 | 0.010601 | 0.039834 | 0.010908 | 0.041044 |
| 131 | 0.013991 | 0.053824 | 0.014384 | 0.055428 |
| 130 | 0.018220 | 0.072044 | 0.018757 | 0.074185 |
| 129 | 0.023498 | 0.095542 | 0.024114 | 0.098299 |
| 128 | 0.029866 | 0.125408 | 0.030603 | 0.128901 |
| 127 | 0.037288 | 0.162696 | 0.038228 | 0.167130 |
| 126 | 0.045771 | 0.208467 | 0.046898 | 0.214027 |
| 125 | 0.055165 | 0.263632 | 0.056310 | 0.270337 |
| 124 | 0.064853 | 0.328485 | 0.066020 | 0.336357 |
| 123 | 0.074178 | 0.402662 | 0.075236 | 0.411593 |
| 122 | 0.081929 | 0.484591 | 0.082885 | 0.494479 |
| 121 | 0.087158 | 0.571750 | 0.087696 | 0.582174 |
| 120 | 0.088520 | 0.660269 | 0.088559 | 0.670734 |
| 119 | 0.084982 | 0.745252 | 0.084406 | 0.755140 |
| 118 | 0.076454 | 0.821705 | 0.075245 | 0.830385 |
| 117 | 0.063606 | 0.885312 | 0.061851 | 0.892236 |
| 116 | 0.048069 | 0.933381 | 0.046111 | 0.938347 |
| 115 | 0.032432 | 0.965813 | 0.030604 | 0.968952 |
| 114 | 0.019117 | 0.984930 | 0.017664 | 0.986616 |
| 113 | 0.009567 | 0.994496 | 0.008614 | 0.995230 |
| 112 | 0.003894 | 0.998390 | 0.003420 | 0.998650 |
| 111 | 0.001257 | 0.999647 | 0.001065 | 0.999715 |
| 110 | 0.000297 | 0.999944 | 0.000243 | 0.999958 |
| 109 | 0.000050 | 0.999994 | 0.000038 | 0.999996 |
| 108 or Less | 0.000006 | 1.000000 | 0.000004 | 1.000000 |
Count of the Hottest Numbers in 300 Spins in Double-Zero Roulette
What if you don't want to spend 100 hours gathering data on a single wheel? Some casinos are kind enough to give you, on a silver platter, the number of times in the last 300 spins the four 'hottest' and 'coolest' numbers occurred. The image at the top of the page shows an example taken on a double-zero wheel at the Venetian.
In 300 spins, the average number of wins on a double-zero wheel for any number is 300/38=7.9. As you can see from the image above, the four hottest numbers were 20, 5, 29, and 2, which occurred 15, 14, 13, and 12 times respectively. Is this unusual? No. In a simulation of over 80 billion spins, the most frequent number, in 300-spin experiments, appeared most frequently at 14 times with a probability of 27.4%. The most likely total of the second, third, and fourth most frequent numbers was 13, 12, and 12 times respectively, with probabilities of 37.9%, 46.5%, and 45.8%. So the results of the 'hottest' numbers in the image above were a little more flat than average.
The following table shows the probabilities of the four hottest numbers in 300 spins of double-zero roulette. For example, the probability the third most frequent number happens 15 times is 0.009210.
Count of the Hottest Four Numbers in 300 Spins on a Double-Zero Wheel
| Observations | Probability Most Frequent | Probability Second Most Frequent | Probability Third Most Frequent | Probability Fourth Most Frequent |
|---|---|---|---|---|
| 25 or More | 0.000022 | 0.000000 | 0.000000 | 0.000000 |
| 24 | 0.000051 | 0.000000 | 0.000000 | 0.000000 |
| 23 | 0.000166 | 0.000000 | 0.000000 | 0.000000 |
| 22 | 0.000509 | 0.000000 | 0.000000 | 0.000000 |
| 21 | 0.001494 | 0.000001 | 0.000000 | 0.000000 |
| 20 | 0.004120 | 0.000009 | 0.000000 | 0.000000 |
| 19 | 0.010806 | 0.000075 | 0.000000 | 0.000000 |
| 18 | 0.026599 | 0.000532 | 0.000003 | 0.000000 |
| 17 | 0.060526 | 0.003263 | 0.000060 | 0.000001 |
| 16 | 0.123564 | 0.016988 | 0.000852 | 0.000020 |
| 15 | 0.212699 | 0.071262 | 0.009210 | 0.000598 |
| 14 | 0.274118 | 0.215025 | 0.068242 | 0.011476 |
| 13 | 0.212781 | 0.379097 | 0.283768 | 0.117786 |
| 12 | 0.067913 | 0.270747 | 0.464748 | 0.457655 |
| 11 | 0.004615 | 0.042552 | 0.168285 | 0.383900 |
| 10 | 0.000017 | 0.000448 | 0.004830 | 0.028544 |
| 9 | 0.000000 | 0.000000 | 0.000001 | 0.000020 |
| Total | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
The next table shows the mean, median, and mode for the count of the first, second, third, and fourth hottest numbers in millions of 300-spin simulations of double-zero roulette.
Summary of the Count of the Four Most Frequent Numbers in 300 Spins of Double-Zero Wheel
| Order | Mean | Median | Mode |
|---|---|---|---|
| First | 14.48 | 14 | 14 |
| Second | 13.07 | 13 | 13 |
| Third | 12.27 | 12 | 12 |
| Fourth | 11.70 | 12 | 12 |
Count of the Coolest Numbers in 300 Spins in Double-Zero Roulette
The next table shows the probability of each count of the four collest numbers in 300 spins of double-zero roulette.
Count of the Coolest Four Numbers in 300 Spins on a Double-Zero Wheel
| Observations | Probability Least Frequent | Probability Second Least Frequent | Probability Third Least Frequent | Probability Fourth Least Frequent |
|---|---|---|---|---|
| 0 | 0.012679 | 0.000063 | 0.000000 | 0.000000 |
| 1 | 0.098030 | 0.005175 | 0.000135 | 0.000002 |
| 2 | 0.315884 | 0.088509 | 0.012041 | 0.001006 |
| 3 | 0.416254 | 0.420491 | 0.205303 | 0.063065 |
| 4 | 0.150220 | 0.432638 | 0.595139 | 0.522489 |
| 5 | 0.006924 | 0.052945 | 0.185505 | 0.401903 |
| 6 | 0.000008 | 0.000180 | 0.001878 | 0.011534 |
| Total | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
The next table shows the mean, median, and mode for the count of the first, second, third, and fourth coolest numbers in the 300-spin simulations of double-zero roulette.
Summary of the count of the Four Least Frequent Numbers on a Double-Zero Wheel
| Order | Mean | Median | Mode |
|---|---|---|---|
| Least | 2.61 | 3 | 3 |
| Second Least | 3.44 | 3 | 4 |
| Third Least | 3.96 | 4 | 4 |
| Fourth Least | 4.36 | 4 | 4 |
Count of the Hottest Numbers in 300 Spins of Single-Zero Roulette
In 300 spins, the average number of wins on a single-zero wheel for any number is 300/37=8.11. The next table shows the probability of each count of the four coolest numbers in 300 spins of double-zero roulette. For example, the probability the third most frequent number happens 15 times is 0.015727.
Count of the Hottest Four Numbers in 300 Spins on a Single-Zero Wheel
| Observations | Probability Most Frequent | Probability Second Most Frequent | Probability Third Most Frequent | Probability Fourth Most Frequent |
|---|---|---|---|---|
| 25 or More | 0.000034 | 0.000000 | 0.000000 | 0.000000 |
| 24 | 0.000078 | 0.000000 | 0.000000 | 0.000000 |
| 23 | 0.000245 | 0.000000 | 0.000000 | 0.000000 |
| 22 | 0.000728 | 0.000000 | 0.000000 | 0.000000 |
| 21 | 0.002069 | 0.000002 | 0.000000 | 0.000000 |
| 20 | 0.005570 | 0.000018 | 0.000000 | 0.000000 |
| 19 | 0.014191 | 0.000135 | 0.000000 | 0.000000 |
| 18 | 0.033833 | 0.000905 | 0.000008 | 0.000000 |
| 17 | 0.074235 | 0.005202 | 0.000125 | 0.000001 |
| 16 | 0.144490 | 0.025286 | 0.001624 | 0.000050 |
| 15 | 0.232429 | 0.097046 | 0.015727 | 0.001286 |
| 14 | 0.269735 | 0.259360 | 0.101259 | 0.021054 |
| 13 | 0.177216 | 0.382432 | 0.347102 | 0.175177 |
| 12 | 0.043266 | 0.208137 | 0.429715 | 0.508292 |
| 11 | 0.001879 | 0.021373 | 0.102979 | 0.283088 |
| 10 | 0.000003 | 0.000103 | 0.001461 | 0.011049 |
| 9 | 0.000000 | 0.000000 | 0.000000 | 0.000002 |
| Total | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
The next table shows the mean, median, and mode for the count of the first, second, third, and fourth hottest numbers in millions of 300-spin simulations of double-zero roulette.
Summary — Count of the Four Hottest Numbers — Double-Zero Wheel
| Order | Mean | Median | Mode |
|---|---|---|---|
| First | 14.74 | 15 | 14 |
| Second | 13.30 | 13 | 13 |
| Third | 12.50 | 12 | 12 |
| Fourth | 11.92 | 12 | 12 |
Count of the Coolest Numbers in 300 Spins in Single-Zero Roulette
The next table shows the probability of each count of the four coolest numbers in 300 spins of double-zero roulette. For example, the probability the third coolest numbers will be observed five times is 0.287435.
Count of the Coolest Four Numbers in 300 Spins on a Double-Zero Wheel
| Observations | Probability Least Frequent | Probability Second Least Frequent | Probability Third Least Frequent | Probability Fourth Least Frequent |
|---|---|---|---|---|
| 0 | 0.009926 | 0.000038 | 0.000000 | 0.000000 |
| 1 | 0.079654 | 0.003324 | 0.000068 | 0.000001 |
| 2 | 0.275226 | 0.062392 | 0.006791 | 0.000448 |
| 3 | 0.419384 | 0.350408 | 0.140173 | 0.034850 |
| 4 | 0.200196 | 0.484357 | 0.557907 | 0.406702 |
| 5 | 0.015563 | 0.098547 | 0.287435 | 0.521238 |
| 6 | 0.000050 | 0.000933 | 0.007626 | 0.036748 |
| 7 | 0.000000 | 0.000000 | 0.000001 | 0.000013 |
| Total | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
The next table shows the mean, median, and mode for the count of the first, second, third, and fourth coolest numbers in the 300-spin simulations of single-zero roulette.
Summary of the count of the Four Least Frequent Numbers on a Single-Zero Wheel

| Order | Mean | Median | Mode |
|---|---|---|---|
| Least | 2.77 | 3 | 3 |
| Second Least | 3.62 | 4 | 4 |
| Third Least | 4.15 | 4 | 4 |
| Fourth Least | 4.56 | 5 | 5 |
The least I hope you have learned from this article is it is to be expected that certain numbers will come up more than others. To put it in other words, it is natural that some numbers will be 'hot' and some 'cool.' In fact, such differences from the mean are highly predictable. Unfortunately, for roulette players, we don't know which numbers will be 'hot,' just that some of them almost certainly will be. I would also like to emphasize, contrary to the Gambler's Fallacy, that on a fair roulette wheel that every number is equally likely every spin and it makes no difference what has happened in the past.
Finally, it should not be interpreted that we give an endorsement to the 888 Casino, which we linked to earlier. I am very bothered by this rule in their rule 6.2.B. Before getting to that, let me preface with a quote from rule 6.1, which I'm fine with.
'If we reasonably determine that you are engaging in or have engaged in fraudulent or unlawful activity or conducted any prohibited transaction (including money laundering) under the laws of any jurisdiction that applies to you (examples of which are set out at section 6.2 below), any such act will be considered as a material breach of this User Agreement by you. In such case we may close your account and terminate the User Agreement in accordance with section 14 below and we are under no obligation to refund to you any deposits, winnings or funds in your account.' -- Rule 6.1
Let's go further now:
Best Casino Roulette Numbers Game
The following are some examples of 'fraudulent or unlawful activity' -- Rule 6.2
Next, here is one of many examples listed as rule 6.2.B
'Unfair Betting Techniques: Utilising any recognised betting techniques to circumvent the standard house edge in our games, which includes but is not limited to martingale betting strategies, card counting as well as low risk betting in roulette such as betting on red/black in equal amounts.' -- Rule 6.2.B
Let me make it perfectly clear that all betting systems, including the Martingale, not only can't circumvent the house edge, they can't even dent it. It is very mathematically ignorant on the part of the casino to fear any betting system. Why would any player trust this casino when the casino can seize all their money under the reason that the player was using a betting system? Any form of betting could be called a betting system, including flat betting. Casino 888 normally has a pretty good reputation, so I'm surprised they would lower themselves to this kind of rogue rule.
Written by: Michael Shackleford